本文中，我们纵览Transformer和胶囊网络的主要模块并尝试画出两个模型不同部分的联系。这里的目标是理解两者是否本质上不同，亦或他们有什么关联。 译自Samira Abnar's Post

Transformers(变压器网络)

Transformers或者叫它自注意力网络，是一系列的深度神经网络结构，其主要特征是堆叠自注意力层以学习输入符号的关于上下文的表示。这些模型已经实现了很多视觉和自然语言处理任务的最优效果。有很多关于Transformer具体实现的细节，但是总体上，Trnasformer是一个编码-解码结构，它的编码和解码模块分别由一组堆叠的自注意力层构成，而在每一层，其学习(重新)计算每一个输入符号的表示。这个表示由对前一层所有输出的符号计算得到。如下图所示

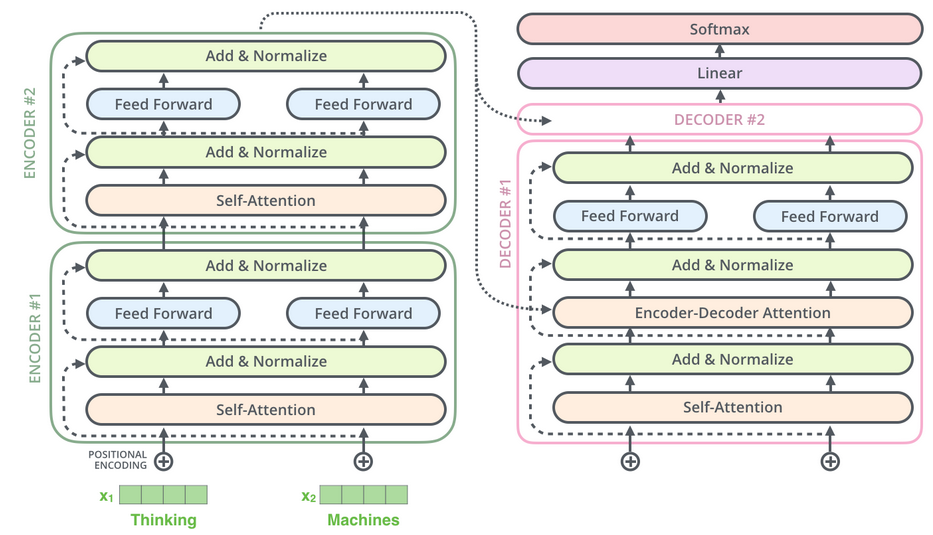
因此，为了得到L+1层的表示，网络将L层的表示通过一个自注意力模块，对于每一个符号模块用其他所有符号L层的表示来更新这个符号的表示而得到L+1层的表示。在解码器中未来的符号是被遮挡的。除了自注意力以外，在解码器还有编解码器间注意力,详见 https://jalammar.github.io/illustrated-transformer/ 。

Transformer的关键部分是自注意力，自注意力有一个重要属性是多头注意力机制。这里我们主要聚焦于这个模块并随着与胶囊网络的比较挖掘它的细节。

之所以使用多头注意力的主要动机是得到更多表征子空间的机会，是因为每个注意力头(注意力输出)得到表示一个不同角度的映射。在理想情况下，每个头将通过从一个不同方向带入计算来得到输入表示的不同部分。并且在实践中，不同的注意力头计算出了不同的注意力分布。Transformer中的多个注意力头就像卷积神经网络中的多个卷积核。

这里，我们展开讲信息如何从L层的不同位置通过多头自注意力计算得到L+1层的表示。

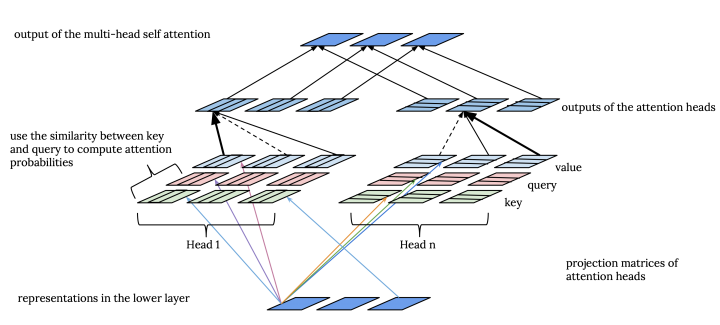
首先，我们应该知道每一层每个位置的所谓的表示是一个形如(键，值，问)三元组。因此，每一层由三个权重矩阵(K,Q,V)，矩阵的每行对应一个位置。

每个注意力头i的输入是K、Q、V的变换: \( K_i = W_k^{i}K, V_i = W_v^{i}V, Q_i = W_q^{i}Q \)

然后，注意力头i的输出是: \( attention_i(K_i,Q_i,V_i) = softmax(\frac{Q_iK_i^T}{\sqrt{d_i}})V_i \) 其中d_i是K_i的维度。

直觉上，L+1层每个位置的表示，是L层每个表示的加权和。每个注意力头计算L+1层每个位置的问(query)和L层每个位置的键的相似性，然后通过softmax函数将相似性数值归一化得到注意力分布。因此自注意力层每个头每个位置都有一个关于前一层的注意力分布。每个注意力头最终通过注意力分布加权上一层的值得到输出。最后，将所有注意力头的输出拼接后经过线性变换得到多头注意力最终的输出。

\[ multiattention(K,Q,V) = [attention_i(K_0,Q_0,V_0), ... , attention_i(K_m,Q_m,V_m) ]W_o \]

所以那些需要学习的参数有每层最后的变换矩阵 $W_o$ 和每层每个注意力头的三个变换矩阵 $W_k,W_q,W_v$ 。

通过期望最大化路由矩阵胶囊组 Matrix Capsules with EM routing

胶囊网络起先被提出用于以更自然的方式处理图像。2000年Hinton和Ghahramani认为依赖于独立的预处理阶段的图像识别系统会受到这样的事实的困扰，即分割器不了解目标的一般信息，并提出一个同时识别和分割的系统。这个设想是，为了识别目标对象的各个部分，您首先需要对目标是什么有一个大体的了解。换句话说，我们需要同时由自上而下和自下而上的信息流。例如自然语言处理中解析园径句型。胶囊网络可以被视作一个卷积核输出和池化被动态路由取代的卷积神经网络。

胶囊是学习在有限的观测条件下检测隐式定义的实体的单元。它既输出实体的出现概率，又输出反映实体特征（例如姿态信息）的“实例参数”。出现概率是视点不变的，例如它不会随着实体的移动或旋转而改变，而实例参数是视点等变的，例如如果实体移动或旋转它们就会改变。

在ICLR2018通过期望最大化路由矩阵胶囊组中，他们使用了一个由一个标准卷积层、一个主胶囊层以及后续几个卷积胶囊层组成的胶囊网络。在这个版本的胶囊网络中，实例参数被表示为一个成为姿态矩阵的矩阵。

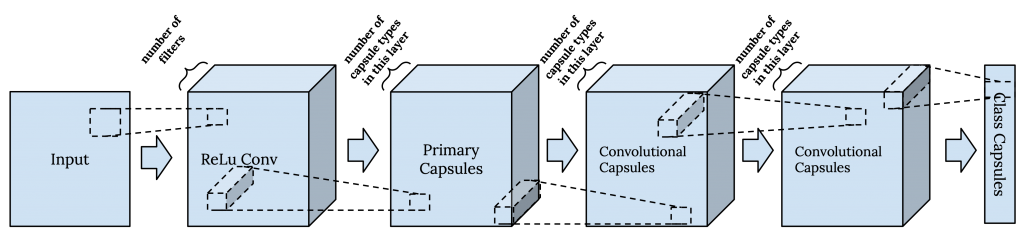
每个胶囊层由固定某个超参数数目种类的胶囊(像卷积网络的滤波器)，一个胶囊是某种胶囊类型的实例。每种胶囊类型对应一个实体，并且相同种类的胶囊在不同位置提取同一个实体。在较低层中的各胶囊类型识别低层次的实体，如眼睛，在较高层中的各胶囊类型呈现更高级的实体，如脸。

在卷积胶囊层，每中胶囊的权重矩阵都和输入卷积，就像卷及网络中的卷积核(滤波器)那样。

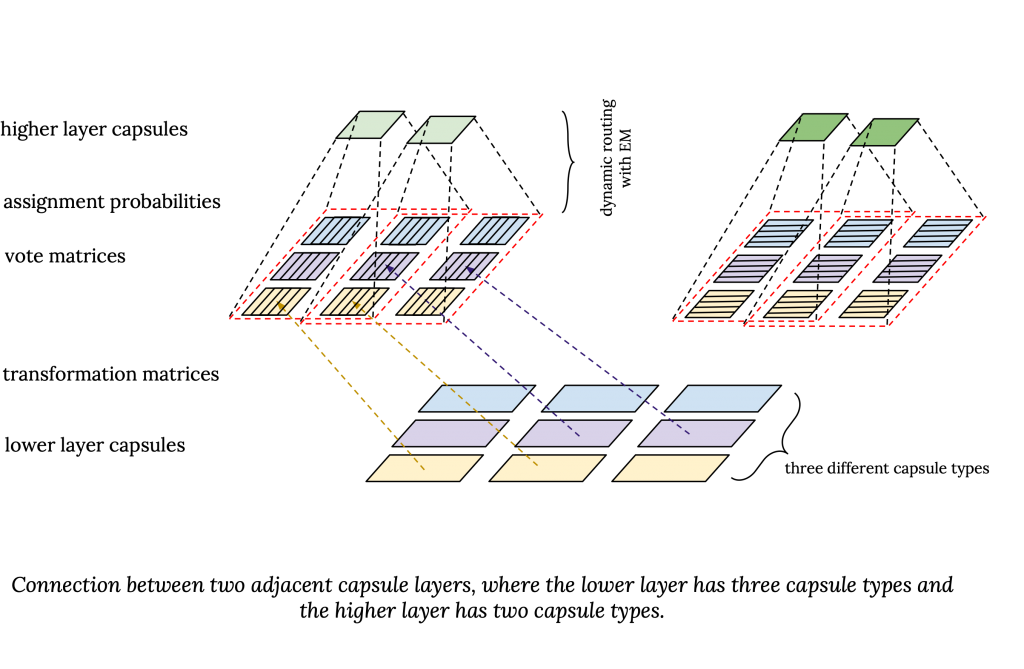
在胶囊网络，每层的胶囊种类数是预定义的。在相邻层的各种胶囊间有一个变换矩阵。这样每个上层的胶囊从不同的角度看下层胶囊中的实体。

姿态矩阵

下面的方程表示如何从底层胶囊输出Mi计算得到高层胶囊输出Mj:

\[ M_{j} = \sum_{i}{r_{ij}W_{ij}M_{i}} \]

方程中, $r_{ij}$ 表示胶囊i到胶囊j的 分配概率 ，或者说是胶囊i对胶囊j的贡献。$W_{ij}Mi$ 是低层姿态矩阵在高层的投影，也叫做“投票矩阵” $V{ij}$。所以高层胶囊的姿态矩阵是低层胶囊的投票矩阵的加权平均。注意分配概率通过动态路由的期望最大化过程算出，不同于胶囊的出现概率或者激活概率。

出现概率

现在让我们看看高层胶囊的激活概率是如何计算的。简单的说，一个高层胶囊的激活概率由激活它的成本与不激活它的成本的差决定。

\[ a_j \propto cost(j|active=false) - cost(j|active=true) \]

问题是这些成本是什么，我们该如何计算它们？

如果一个高层胶囊的分配概率和大于0，例如有一些低层胶囊被分配给这个高层胶囊，则存在不激活该胶囊的成本。但是胶囊的激活概率并非仅由分配概率的值来计算。我们还应该考虑分配给高层胶囊的低层胶囊的投票矩阵间的一致性。

换句话说，分配给该高层胶囊的低层胶囊应该是该高层胶囊应表示的实体的某些部分。因此激活胶囊的成本还反映了较低层胶囊的投票矩阵与为较高层胶囊计算的姿势矩阵之间的不一致程度。另外，为了避免琐碎地激活胶囊，激活每个胶囊有固定的惩罚。

通过期望最大化动态路由

这里的主要挑战是计算分配概率 $r_ {ij}$ 。这基本上意味着如何将较低层的胶囊 $\OmegaL$ 连接到较高层的胶囊 $\Omega{L+1}$ ，或者说，如何在胶囊层之间路由信息。我们希望这些连接不仅取决于下层胶囊的存在，还取决于它们彼此之间以及与上层胶囊的相关性。例如，代表眼睛的胶囊（是面部的一部分）可能不应该连接到代表桌子的胶囊。这可以看作是计算从较低层胶囊到较高层胶囊的注意力。问题是，我们事先没有较高级别胶囊的初始表示，因此能够基于较低层胶囊与较高层胶囊的相似性来计算此概率。这是因为胶囊的表示取决于将要分配来自下层的哪些胶囊。这正是动态路由切入并使用期望最大化解决问题的地方。

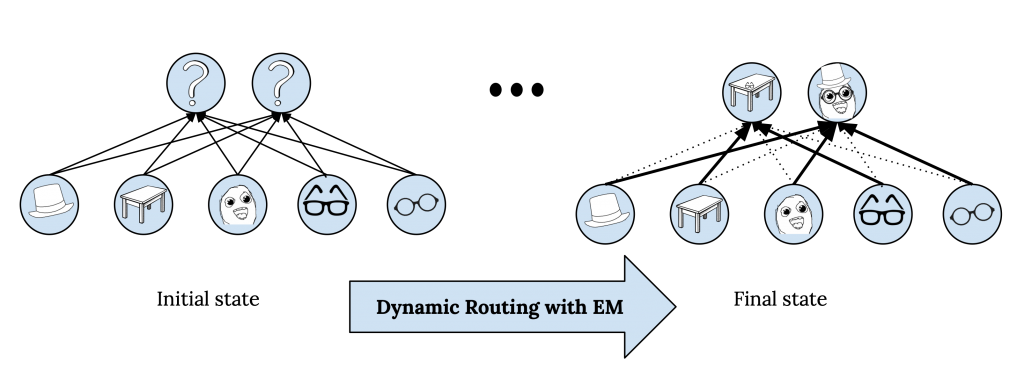
我们能用期望最大化算法由L层的表示及其分配对L+1层的分配概率计算L+1层的表示。这个迭代过程叫做通过期望最大化动态路由。注意通过期望最大化的动态路由是胶囊网络前向传播的一部分，训练时，误差通过展开的动态路由迭代反向传播。

值得注意的是，主胶囊层的计算有些不同，因为它们下面的层不是胶囊层。主胶囊的姿态矩阵只是下层卷积核输出的线性变换，它们的激活是同一组下层核输出的加权和的sigmoid函数。此外，最后一个胶囊层由每个输出类别的一个胶囊组成。将最后一个卷积胶囊层连接到最后一层时，转换矩阵在不同位置共享，并且它们使用一种称为“坐标附加”的技术来保留有关卷积胶囊位置的信息。

胶囊网络对比Transformers

最后，我们进入最有趣的部分——比较这两种模型。尽管从实现的角度看，胶囊网和Transformer似乎不太相似，但这两个模型系列的不同组件之间在功能上有一些相似之处。

动态路由对比注意力

在胶囊网络中，我们使用动态路由来确定从较低层到较高层的连接，与此相对，在Transformer中我们采用自注意力来决定如何关注输入的不同部分以及来自不同部分的信息如何对表示的更新其作用。我们可以将Transformer中的注意力权重对应到胶囊网络中的分配概率，然而，在胶囊网络中分配概率是自下而上计算的，而在Transformer中注意力是自上而下计算的。即，Transformer中的注意力权重分布在较低层的表示上，但是在胶囊网络中，分配概率分布在较高层的胶囊上。请注意，的确是在Transformer中，注意力概率是基于同一层中表示形式的相似性计算的，但这等效于以下假设：较高层首先使用较低层的表示形式进行初始化，然后再根据将初始表示与较低层的表示进行比较而计算出的注意力概率进行更新。

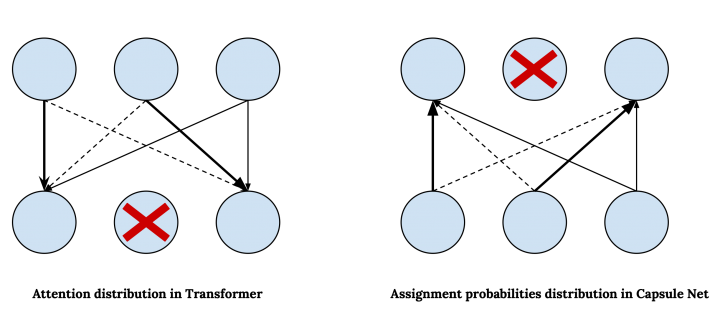
胶囊网自下而上的注意力以及存在概率和激活胶囊的惩罚，明确允许模型在信息传播到更高层时抽象出概念。另一方面，在Transformer中，自上而下的关注机制允许较高层中的节点不参与较低层中的某些节点，并过滤掉在这些节点捕获的信息。

现在，问题是为什么胶囊网络需要期望最大化来动态路由？为什么我们不能用类似于Transformer中计算注意力的机制来计算胶囊网络的分配概率？

想当然，我们可以使用点积相似度来计算较低层胶囊与较高层胶囊的相似度以计算分配概率。

挑战在于在胶囊网中，由于高层胶囊应该表示的是事先未知的东西，我们对高层胶囊的表示没有任何先验假设。另一方面，在Transformer中，所有层中的节点数相同且等于输入符号的数量，因此我们可以将每个节点解释为相应输入符号的上下文表示。这使我们可以使用来自较低层的表示来初始化每个较高层中相应的表示，进而使用表示之间的相似性分数来计算注意力权重。

胶囊类型和注意力头

胶囊网和Transformer结构都具有一种机制，该机制允许模型从不同的角度从较低的层处理表示以计算较高层的表示。在胶囊网中，来自两个相邻层的每对胶囊类型之间存在不同的转换矩阵，因此作为不同胶囊类型的实例的胶囊从不同的角度查看了上一层中的胶囊。与此相对，在Transformer中，我们有多个注意力头，每个注意力头使用一组不同的转换矩阵来计算键，值和问的投影。所以，每个注意头都在下层表示的不同投影上工作。这两种机制与在卷积神经网络中具有不同内核的目的相似。

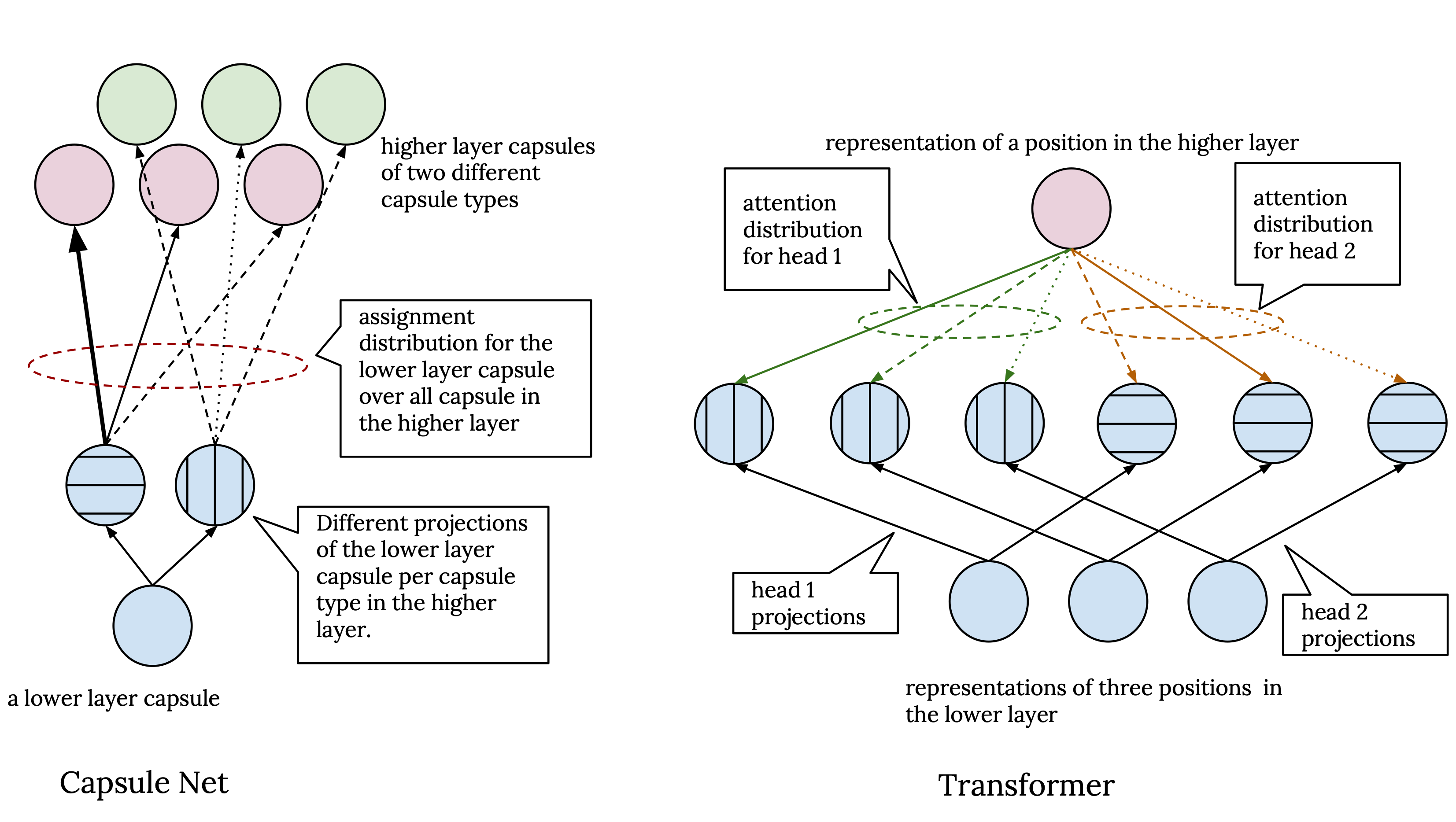
现在，胶囊网络和Transformer之间的不同之处在于，在胶囊网络中，尽管不同类型的胶囊具有不同的视点，但最终，在所有胶囊上对下层胶囊的分配概率进行了归一化 不管它们的类型如何。因此，在下层每个胶囊都有一个分配分布。而在Transformer中，每个注意力头都独立处理其输入。这意味着我们对于上层中的每个位置都有单独的注意力分布，并且注意力头的输出仅在最后一步中进行组合，在此步骤中，它们被简单地连接起来并进行线性变换以计算多头注意力模块的最终输出。

位置编码和坐标附加

在Transformer和胶囊网络中，都有某种机制可以将特征的位置信息显式添加到模型计算的表示中。然而，在Transformer中这是在第一层之前完成的，第一层输入即是位置编码和词向量的加和，而胶囊网中是在最后一层通过坐标附加完成的，其中每个胶囊的接收区域的放缩后的中心坐标（行，列）被添加到其投票矩阵右侧列的前两个元素中。

结构化的隐表示 Structured hidden representations

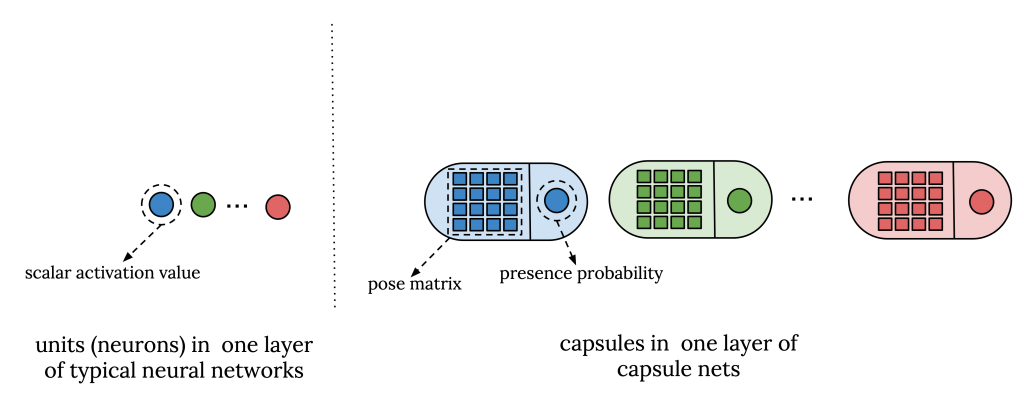
在Transformer和胶囊网络中，隐表示都以某种方式构造。在胶囊网中，用由一个姿态矩阵和一个激活值表示的胶囊代替标准神经网络中的标量激活单元。姿态矩阵对有关每个胶囊的信息进行编码，并用于动态路由以计算较低层胶囊和较高层胶囊之间的相似度，而激活概率决定每个胶囊是否启用。

与此相对，在Transformer中，表示被分解为键，问和值的三元组，其中键和问是寻址向量，用于计算输入不同部分之间的相似度，并计算注意力分布以找到输入的哪些不同部分有助于彼此的表示。

用非常宽松的术语来说，胶囊网络中的姿态矩阵在Transformer中起键和问矢量的作用。这里的要点是，分开编码不同种类信息的表示形式似乎有一些优势，并且在这两种模型中，这都是基于隐状态在路由或注意力过程中的作用来完成的。